When you place one end of a metal spoon in hot water, heat flows from the end submerged in water to the end that is not. The temperature at each point in that spoon when viewed collectively is a scalar field. If a temperature-camera were to capture this spoon, it would look like this.
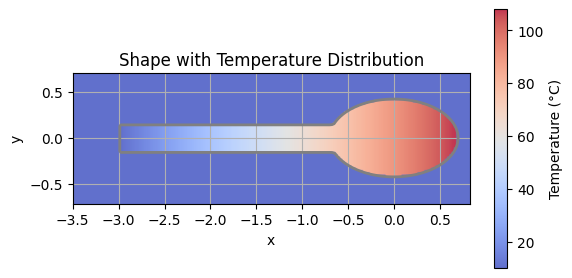
Each point in this scalar field defines a temperature value. It does not show direction at all. But when the gradient of this temperature field is taken, the slope reveals that path with the steepest climb or drop in temperature.
The Vector Operators
Now if you have a vector field and want to determine if it converges, diverges, or rotates, you might think you’d need to plot this field and visually inspect it. While this might give you a solution, a better technique is observing the result of the vector operators, grad, div, and curl.
grad, div, and curl, represented as ∇, ∇∙, and ∇⨯, repsent differential operations done on vectors. grad ∇ is concerned with finding a gradient vector from a scalar. div ∇∙ is concerned with finding a scalar from a vector. curl ∇⨯ is concerned with finding a vector from another vector.
Gradient of a Vector field
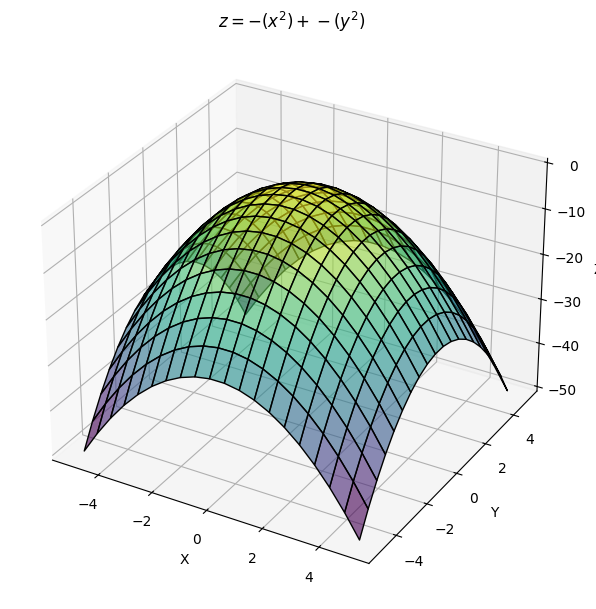
You can visualize a very simple vector field like $z = -(x^2) + -(y^2)$
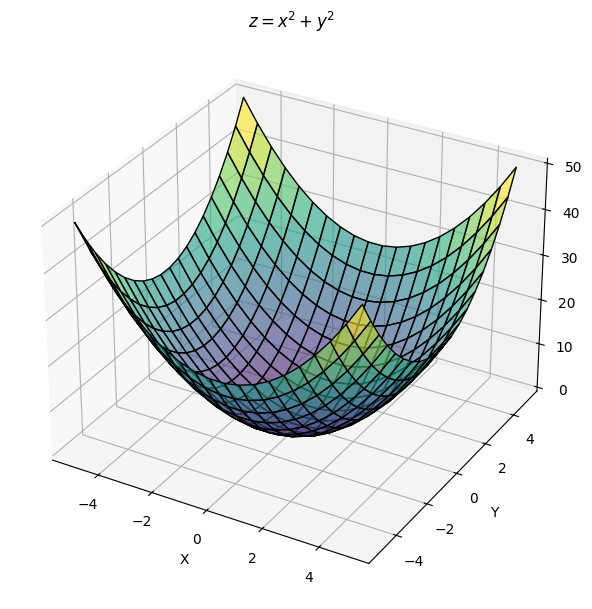
Oh, and the normal version of this equation has the plot look like this
Anyway, so if you consider this equation a vector field, the plot would look like:
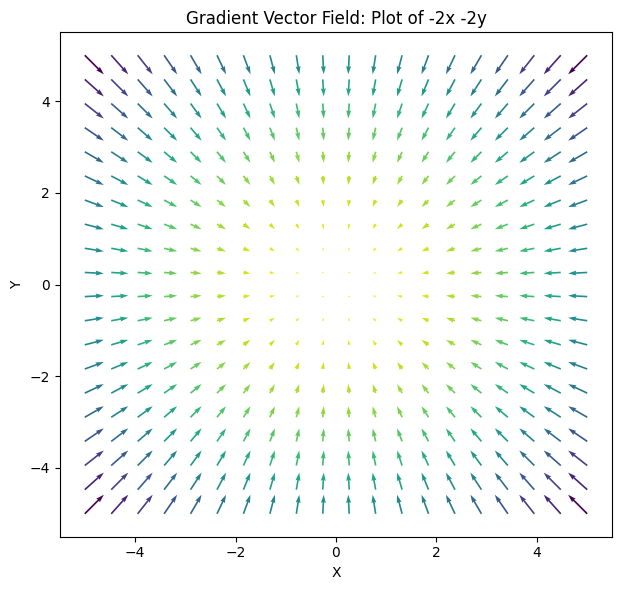
The convergence results from the grad operator which takes partial derivatives of all components in the expression.
$$ \begin{align*} \text{Z} &= -(x^2) + -(y^2) \newline \frac{\partial Z}{\partial x} &= -2x \newline \frac{\partial Z}{\partial y} &= -2y \end{align*} $$
Maxwell’s Equations
Maxwell’s equations form the basis of electromagnetic analysis and ingrain the vector operations: div and curl.
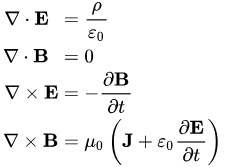
They are a set of partial differential equations that tell us how a charge will behave in a magnetic or electrical field.